热搜关键词: 超声波焊接机 珠海超声波焊接机 超声波塑料焊接机厂家 超声波厂家 灵高超声波
(2)超声波的衍射
分析超声衍射的物理基础是惠更斯(Huygens)原理。该原理由荷兰物理学家惠更斯于 1690年提出。按此原理,媒质中波动传到的各点,都可以看作是发射声波的新波源(或称次波源)。以后时刻的波阵面,可由这些新波源发出的子波波前的包络面做出。
将这一原理运用于衍射问题,可分析声源辐射声场特性,也可解释超声波遇到障碍物时,波阵面发生畸变的现象,下面分远场区和近场区分别讨论。
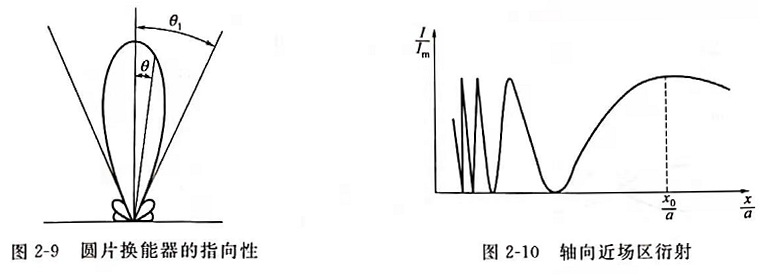
①远场区。设超声波换能器是一小圆片,可以把表面上的每点都看成是振源,衍射出一个小球面波(子波),这些子波是没有指向性的。但离开换能器的空间某一点的声压是这些无数个子波叠加的结果(衍射),却有指向性。指向性用所谓指向性图案来描述(见图2-9)。圆片换能器的指向性图案是由一个主瓣与几个副瓣构成。这些图案的物理意义是θ= 0°时声压极大,θ逐渐增加时,声压减少。通常用θ角处声压对θ=0°时的声压比值表示,其比值叫做指向因素。可以证明
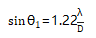
式中,D为声源直径;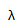 为声波在介质中的波长;
为声波在介质中的波长;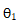 伍为主瓣的半扩散角。
伍为主瓣的半扩散角。
②近场区。在换能器表面附近,由于衍射的结果,沿某轴向各点的声场会周期性地出现极大值和极小值,如图2-10所示。如以I代表离圆片距离x处的声强,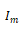 代表声场的极大值,则有
代表声场的极大值,则有
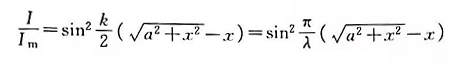
由此得到声强极大值处的坐标为
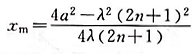
式中,n=为0,1,2,…;a为圆形换能器的半径。最远的极大值相当于n= 0,对应的距离为:
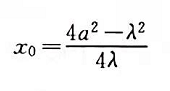
当a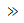 λ时,
λ时,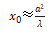 。这说明
。这说明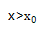 后就不再有声强极大值出现,
后就不再有声强极大值出现,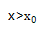 后即进入远场范围。
后即进入远场范围。

![]()
微信咨询

咨询电话