频谱分析模型

       当超声波遇到外形比较尖锐的反射体时(实际情况中大多数缺陷都属于这类反射体)，过去针对声波与球体或有限大小的圆柱体之间的衍射问题发展出的研究方法变得不再适用。为此，Keller[36]提出了一种电磁波衍射原理，对其进行适当的修正有望能够解决二维孔隙或任意形状反射体的衍射问题。

       几何衍射理论假定当声波遇到边界时，除了反射、折射和透射波之外，还存在衍射波。入射波和衍射波与边界的夹角相同，且分别位于入射点处边界法平面的两侧。一束入射波可以产生无限多个衍射波，这些衍射波的轴线均与入射点处缺陷边界的法线方向相同。进一步假定这些衍射波的幅度和相位之间存在内在联系，各束衍射波幅度的变化可以通过能量守恒定律确定。入射波的波场强度可以表达为如下形式:

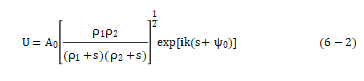
式中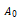， 和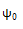 是入射波初始点处的幅度和相位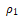；和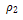 是波前的曲率半径；k为波数；s是声波传播的距离。假定衍射波的能量场正比于入射波的能量场，并引入衍射系数表示这种比例关系。当平面标量波在半无限大平面上发生衍射时，可以得到衍射波的确定解。对该确定解进行渐近展开就可以求得衍射系数。然后，将上述求解结果同按照几何原理求解所得的结果进行比较。任意点处衍射波的能量场强度可以用如下形式表示:

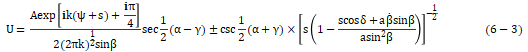
式中，a表示衍射体(缝)的半径; β是入射波与缺陷边界入射点处法线的夹角;是β沿弧长方向的导数; δ是衍射波与缺陷边界入射点处法线的夹角;是入射角；s是入射点到探头之间的距离; a是衍射角。图6-14所示为衍射模型的示意图。在某一给定点处的总衍射场等于该点所有波场的叠加。

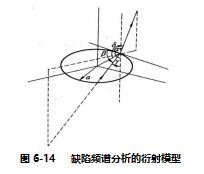
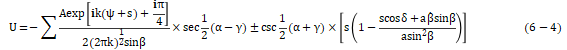
       选用圆盘状衍射体作为研究对象，并且只考虑了存在两列声波时的衍射现象，即仅有来自边界上最近点和最远点的衍射波。设超声波斜入射到位于远场区的半径为a的圆盘状衍射体，对等式(6-4)进行求解，结果如下：

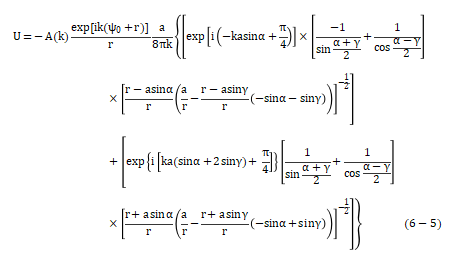
式中，r为圆盘中心与观察点之间的距离；A(k)表示入射波的幅度，它是k(可以是频率)的函数。

       当超声波垂直入射时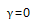，上述表达式可以被大大简化。对于非圆盘状的衍射体，在求解式(6- 4)时需要多于两束的声波来计算β和 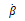的值。式(6-5)在没有进行归一化的情况下，对于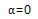的轴向(垂直)散射是不适用的。经过归一化之后，式(6-5)就可以用于解释图6-6中给出的近场区反射波频谱分析的结果了。

       图6-15所示为直径3. 2mm(0.125in)的圆盘状散射体的理论计算结果和实测结果[10]。入射角为0°，衍射角为15°。 观察发现理论和实验结果符合良好。当衍射体为铝试样末端的平底孔时，理论和实验结果同样具有很好的一致性，如图6-16所示[10]。孔的直径为6.4mm(0.25in)，衍射角为25°。

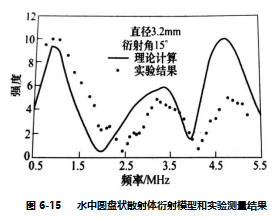
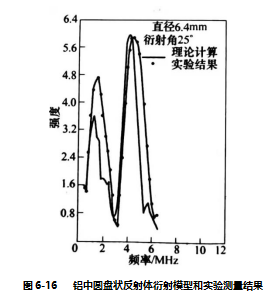
        上述研究结果表明，对于圆盘状反射体，衍射模型能够预测出散射能量随散射角度和超声波频率的变化情况。为了进一步确定缺陷反射体的尺寸和空间取向，引入一个简化模型，即干涉模型。