频谱分析常用定理

       频谱分析中经常要用到一些频谱定理，其实质是傅里叶变换的某些性质，它反映了信号同其频谱之间的基本关系，常用的频谱定理包括[6]:

(1)线性叠加定理   

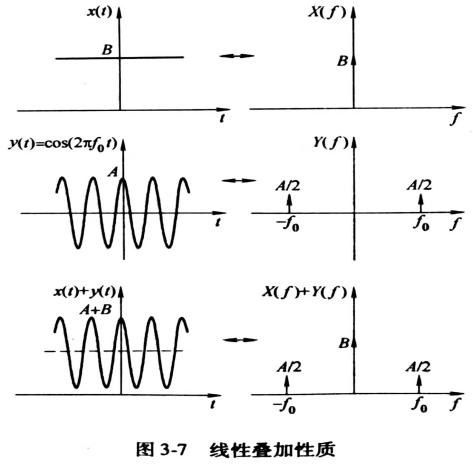
如果x(t)和y(t)分别有傅里叶变换X(f)和Y(f),则它们的和x(t)+y(t)有傅里叶变换X(f) + Y(f),如图3-7所示。

(2)对称或对偶定理   

若时域函数x(t)对应频谱为F(f),即x(t)⟷ F(f)，则有 

(3)时间展缩定理    

如果x(t)的傅里叶变换是F(f)，则x(kt)的傅里叶变换对为

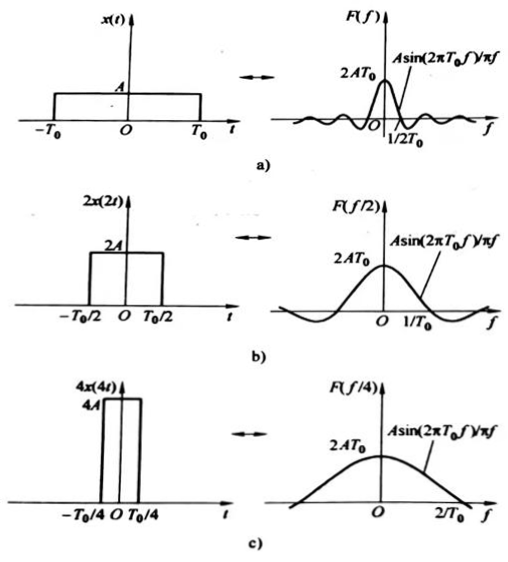
       在科学技术的许多领域，傅里叶变换的时间尺度变化这一性质为大家所熬悉，如图3-8所示，时间尺度扩展(或压缩)h倍，相应于频率尺度压缩(或打辰)h倍。应当指出，当时间尺度扩展时，不仅频率尺度缩小，而且频率域里的垂直幅度增大，使曲线下的面积保持不变。在用磁带机作扩展时间轴和压缩时间轴的频谱分析中，这是一个具有实用价值的方法。

a)时间没有扩展    b）时间放慢2倍，k=1/2   c）时间放慢4倍，k=1/4

(4)频率展缩定理   

如果F(f)的傅里叶变换是x(t)，k是实数，则F(kf)的傅里叶变换可由下面傅里叶变换对给出:

与时间尺度改变相类似，频率尺度扩展(或压缩)k倍，将导致时间尺度压缩(或扩展)k倍。这个效应如图3-9所示。当频率尺度扩展时，时间函数的幅度就增大。

(5)时间位移——时移定理   

如果x(t)的自变量t被移动一个常量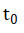,则可

a）频率没扩展  b）频率展缩为1/2，k=1/2   c)频率展缩为1/4，k=1/4

得到

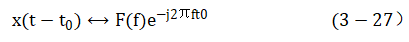
这个变换对的图解如图3-10所示。可以看出，由于时间位移而引起了相角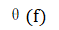的变化，即

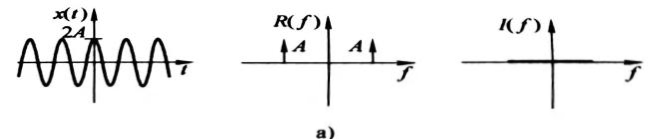
图3-10时间位移性质(续)

   a)没有时移时

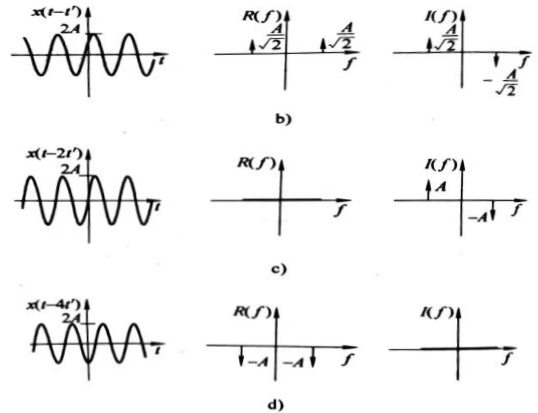
图3-10时间位移性质(续)

b)时移45°时   c）时移90º 时   d）时移180°时

       应该指出，时间位移并不改变傅里叶变换频域幅值的大小。

       灵高超声波起源于1993年，致力于超声波塑焊高端技术应用，集于研发技术、产品制造、销售、服务、全产业链自制的工业超声波技术机器和系统供应商。公司拥有104台CNC加工设备，为客户供应中山超声波焊接机、江门超声波焊接机、阳江超音波设备配件等、根据厂家需求定制非标设备，会和顾客一起从最开始的生产规划逐渐，寻找最好的生产工艺流程和生产线设备。长期以来，产品广泛运用在塑料、医疗器械、3C电子、汽配行业等多个领域。为海内外各大企业，提供高品质。超声波焊接设备及行业应用方案。未来，我们将继续发挥资源、技术、市场等多方面的优势䟡砺前行，引领中国超声波塑焊接技术发展。