倒频谱

       倒频谱(cepstrum)可以用来分析复杂频谱图上的周期成分，分离和提取在密集泛频信号中的成分。在分析具有同族谐频和异族谐频等复杂信号时，效果很好。目前倒频谱已在对语言分析中的语言音调测定、检测机械振动谱图中的谐波分量作故障检测和诊断，以及排除回波等方面得到实际应用。倒频谱分析包括功率倒频谱(power cepstrum)分析和复倒频谱(complex cepstrum)分析两种主要形式，此处仅介绍功率倒频谱。

       功率倒频谱的定义为“对数功率谱的功率谱”，其表达式为

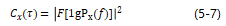
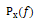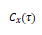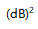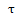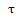式中，为信号的自功率谱； 为功率倒频谱，单位为；F表示傅里叶变换；自变量称为倒频率，具有时间的量纲。一般说来，大的 值称为高倒频率，表示在频谱图上的快速波动和密集谐频:与此相反，小的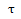值称为低倒频率，表示在频谐图上的缓慢波动和离散谐频。

        实际工程中常用的倒频谱表达式为

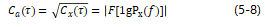
式中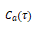，被称为幅值倒频谱，或简称为倒频谱，单位为dB。

       倒频谱实际上是频域信号取对数的傅里叶变换再处理，又称为“频域信号的傅里叶再变换”。对功率谱密度函数取对数的目的是为了使再变换后信号的能量更加集中。

       由于功率倒频谱是对频谱作谱分析得到的，因此，它与自相关函数有关。功率倒频谱与自相关函数具有类似的结构形式和相同的自变量，两者的主要区别在于功率倒频谱是对功率谱作对数转换(即转换成分贝)后再进行傅里叶变换，而自相关函数则是由功率谱函数在线性坐标上的傅里叶变换得到的。由于倒频谱在功率谱的对数转换时，给低幅值分量有较高的加权，可以帮助判别谱的周期性，又能精确地测出频率间隔，因此在某些场合使用倒频谐而不用自相关函数，同时，因为相关函数检测回波的峰值与频谱形状的关系十分密切，经过滤波后(如地震波通过地球传输)实际上不可能加以检测。而功率谱的对数通常对这种滤波的带宽不敏感，所以，在自相关函数无法分辨的场合，功率倒频谱往往还能显示出延时峰。对这种整个谱的形状不敏感性使倒频谱获得了许多应用。

        图5-12是元音“a”的对数谱和倒频谱。由图中可以看到，信号中包含有大量谐波分量，谐波间距等于语音音调；此外，存在许多共振峰，即所谓的构成成分，它由声道的形状决定，并确定了特定的元音声。

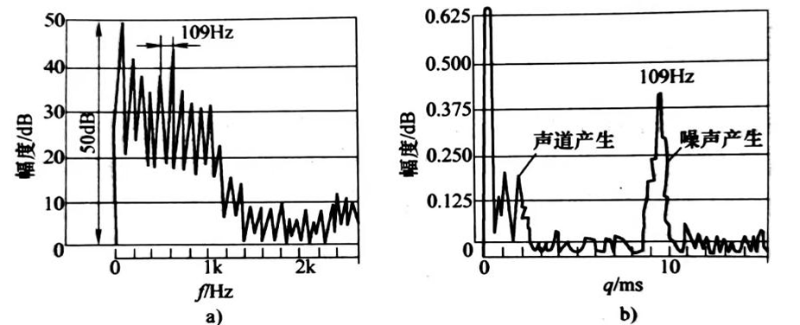
图5-12  元音“a”的对数谱和倒频谱分析

a）对数谱  b)倒频谱

设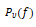为声道内发出的语音信号的功率谱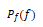， 为共振噪声成分的功率谱，两者合成的元音声的功率谱为

若以对数形式表达，则上式可改写成

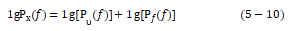
因为傅里叶变换的线性特性，所以在倒频谱中两个函数仍保持相加的关系，并简写成

从图5-12b中可以看出，由声道产生的构成成分与由噪声产生的语音特征，在倒频谱中处于完全不同的位置，能够明显地区别开来。

       此外，在对信号进行频谱分析过程中，还有一些实际问题需要考虑，需要进行所谓的预处理。预处理的基本方法有预滤波、零均值的变换、移动趋势项和信号求平均值等。当信号需要平滑或抑制不需要的频率分量时，可采用滤波的方法；零均值的变换可以简化数字信号处理过程，通过变换使数据的平均值为零;移动趋势项可以避免对峰值的错判以及防止对功率谱计算不准确。详细内容请参考相关资料。

       代名词๓:

       从图5-12b中可以看出，由声道产生的构成成分与由噪声产生的语音特征，在倒频谱中处于完全不同的位置，能够明显地区别开来。

       此外，在对信号进行频谱分析过程中，还有一些实际问题需要考虑，需要进行所谓的预处理。预处理的基本方法有预滤波、零均值的变换、移动趋势项和信号求平均值等。当信号需要平滑或抑制不需要的频率分量时，可采用滤波的方法;零均值的变换可以简化数字信号处理过程，通过变换使数据的平均值为零;移动趋势项可以避免对峰值的错判以及防止对功率谱计算不准确。详细内容请参考相关资料。