热搜关键词: 超声波焊接机 珠海超声波焊接机 超声波塑料焊接机厂家 超声波厂家 灵高超声波
变截面杆纵振动的波动方程
物体在弹性介质中发生振动时会引起介质的振动,对于所有固体在研究振动波时都可以看作是弹性体,由于介质各点之间存在着弹性的联系,一点振动时,相邻各点将被带动依次振动起来,这样,物体的振动就在弹性介质中传播出去,这种物体的振动在弹性介质中的传播被称为波动。本章以质点和简单机械振动系统的振动及超声波的传播原理为理论基础,建立数学模型,根据牛顿定理确定变截面杆纵振动的波动方程。
为了研究方便设定理想状态,假定变截面杆是由均匀、各向同性材料所构成的,略去机械损耗,当杆的横截面尺寸远小于波长时,可以认定,平面纵波沿杆轴向传播,在杆的横截面上应力分布是均匀的。
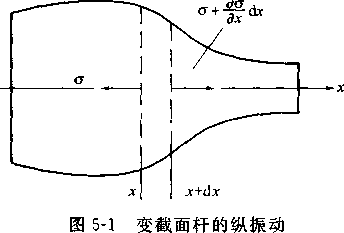
如图5-1所示,任一变截面杆,其对称轴为x轴,任选一小体积元(x,x+dx所限定的区间)作用其上的张应力为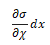 ,根据牛顿定律可以得出动力学方程
,根据牛顿定律可以得出动力学方程
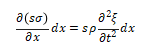
式中,S为杆的横截面积函数,S=S(X);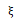 为质点位移函数;
为质点位移函数;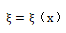 ;
;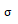 为应力函数;
为应力函数;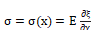 为杆材料的密度;E为杨氏模量。
为杆材料的密度;E为杨氏模量。
在谐振条件下,可以得出变截面杆纵振动的波动方程

式中,k为圆波数,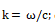
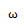 为圆频率;C为纵波在细棒中的传播速度,
为圆频率;C为纵波在细棒中的传播速度,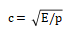 。以下将以波动方程作为基础来讨论单一变幅杆和复合变幅杆的参数计算及形状设计。
。以下将以波动方程作为基础来讨论单一变幅杆和复合变幅杆的参数计算及形状设计。

【本文标签】 纵向振动变幅杆-灵高超声波-超声波变幅杆-超声波焊接设备厂商
【责任编辑】
微信咨询

咨询电话